문제
https://programmers.co.kr/learn/courses/30/lessons/43105
코딩테스트 연습 - 정수 삼각형 | 프로그래머스
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
programmers.co.kr
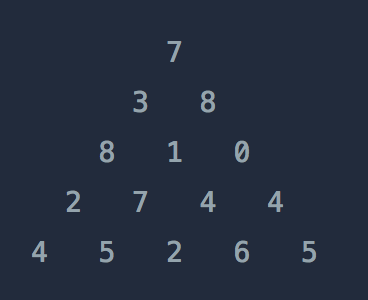
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력
| triangle | result |
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
알고리즘
def solution(triangle):
# 0번째 행은 업데이트 할 필요가 없으므로 생략하고, 1번째 행부터 반복한다.
for i in range(1, len(triangle)):
# 각 행의 원소의 갯수에 대해 반복한다.
for j in range(len(triangle[i])):
# 이 경우는, 각 행의 0번째 원소에 대한 경우이다.
# 인덱스를 잘 살펴보면, 다른 원소와 크기비교를 할 필요 없이 바로 위에 있는 원소의 더해서 덮어쓰면 된다.
if j == 0:
triangle[i][j] = triangle[i][j] + triangle[i-1][j]
# 이 경우는 각 행의 마지막 원소에 대한 경우이다.
# 위와 마찬가지로, 인덱스를 잘 살펴보면 크기비교 필요없이 tri[i-1][j-1]의 값에 해당 원소의 값을 더해서 덮어쓴다.
elif j == len(triangle[i]) - 1:
triangle[i][j] = triangle[i][j] + triangle[i-1][j-1]
# 이 경우는 해당 원소 양옆에 원소들이 있기 때문에, 크기 비교가 필요한 경우이다.
# 최대값을 구해야 하므로, tri[i-1][j-1], tri[i-1][j]와 비교해서 더 큰 값과 tri[i][j]의 값을 더해서 덮어쓴다.
else:
triangle[i][j] = max(triangle[i - 1][j-1], triangle[i - 1][j]) + triangle[i][j]
# 마지막 행에서 가장 큰 값을 리턴한다.
answer = max(triangle[-1])
return answer
설명
이 문제의 경우, 입력의 크기가 행이 최대 500개이고, 각 행은 최대 500개까지의 원소를 갖는다. 따라서, 효율성 테스트를 고려해야 한다. 우리가 DP를 몰랐다면 그냥 모든 경로를 구하고 그 크기가 가장 큰 값을 구하면 되겠지만, 오히려 이렇게 풀면 코드가 더 복잡해지고 효율성도 떨어진다. 그러니까 DP를 이용해보자.
이전 포스팅에서 다뤘던 DP 예제 3번인 동전줍는 로봇문제와 거의 똑같다고 보면 된다. 잘 모르겠다면 아래 링크를 참조하시오.
2020/01/30 - [공부/알고리즘] - [알고리즘 자습]동적계획법(Dynamic Programming) - 동전 선택, 거스름돈 만들기, 동전 줍는 로봇
[알고리즘 자습]동적계획법(Dynamic Programming) - 동전 선택, 거스름돈 만들기, 동전 줍는 로봇
코딩테스트를 준비하면서 여러 문제를 풀다보면, 문제의 입력이 너무 크거나, 반복문과 조건문만으로는 계산하기가 너무 복잡한 경우가 있다. 이런 경우 어거지로 반복문을 돌리면 보통 효율성 테스트를 통과하지..
sexy-developer.tistory.com
예제3번과 다른점이 있다면, 입력으로 주어지는 triangle행렬의 각 행의 원소의 갯수가 다르다는 것이다. 이 점을 좀 자세히 살펴보면, 다음과 같이 풀어야 함을 알 수 있다.
1번 경우: 삼각형에서 왼쪽 변에 있는 원소들을 업데이트하는 법

위 사진에서, 7, 3, 8, 2, 4, 즉 각 행에서 가장 왼쪽에 있는 원소들을 업데이트해야 하는 경우이다. 문제에서 언급했듯이, 각 합을 구하는 경로는 시계방향으로 치면 7시방향으로 내려가거나 5시방향으로 내려가거나 해야 한다. 따라서, 위에 표시한 원소들을 업데이트할 때는, 그 전 행의 첫 원소를 해당 원소에 더하는 식으로 업데이트 하면 된다.

2번 경우: 삼각형에서 오른쪽 변에 있는 원소들을 업데이트하는 법

위 사진에서, 7, 8, 0, 4, 5를 각 단계의 최적값으로 업데이트 해야 하는 경우이다. 이 경우 또한 1번 경우와 마찬가지로, 한쪽 방향으로밖에 내려올 수가 없다. 따라서, 그 전 행의 마지막 원소의 값을 해당 원소에 더해서 업데이트하면 된다.

3번 경우: 나머지 경우

위 사진에서 표시된 나머지 원소들은 업데이트 할 때, 크기 비교를 하면서 업데이트를 해줘야 한다. 이를 그림으로 표현하면 다음과 같다.

위 그림을 보면, 2번째 행의 1번째 원소 1은 그 전 행의 원소 2개로부터 값을 업데이트할 수 있다. 우리는 최대값을 원하므로, 두 값중 큰 값인 15을 골라서, 1을 더한 16를 덮어쓴다.

이렇게 각 원소의 인덱스에 따라 경우를 나누어서, 모든 원소의 값을 업데이트하면 다음과 같은 삼각형이 만들어진다.

결과
올바른 값을 출력한다.

후기
DP 예제를 신경써서 풀어보길 잘했다는 생각이 든다. 타일 장식물도 그렇고, 이번 문제도 그렇고 예제를 한번 꼬아놓은 문제였다. 공책에다가 한줄한줄 써서 정리를 했던 것도 아주 잘했다는 생각이 든다.
다른사람의 코드와도 비교해봤는데, 시간 복잡도도 괜찮은 편이었다. 이렇게 배열을 주고, 최대값 또는 최소값을 찾는 문제는 이렇게 각 원소들을 업데이트해나가면서 최대값을 리턴하는 방식으로 푸는 것이 현명해보인다.
'공부 > 알고리즘' 카테고리의 다른 글
| [프로그래머스 동적계획법/DP]도둑질 - Python3 (Lv.4) (0) | 2020.02.04 |
|---|---|
| [프로그래머스 동적계획법/DP]등굣길 - Python3 (1) | 2020.02.04 |
| [프로그래머스 동적계획법(DP)]타일 장식물- Python3 (0) | 2020.02.04 |
| [알고리즘 자습]동적계획법(Dynamic Programming) - 동전 선택, 거스름돈 만들기, 동전 줍는 로봇 (1) | 2020.01.30 |
| [프로그래머스 힙]라면 공장 - Python3 (0) | 2020.01.29 |



